選択した画像 (a-b)^3+(b-c)^3+(c-a)^3 is equal to 586575-(a-b)^3+(b-c)^3+(c-a)^3 is equal to

Ratios Solved Examples Q 1 On the off chance that ab=23 and bc=57, discover acRatio and Proportion quiz/questions and answers with explanation for various interview, competitive examination and entrance exam/test preparation Solved question papers with detailed answer description, explanation are given in this General Awareness Page 1 Section 84If a b c = 3 4 7, then the ratio (a b c) c is equal to a) 2 1 b) 14 3 c) 7 2 d) 1 2 Solution(By Examveda Team) $$\eqalign{ &\,\,\,\, {\text

Rd Sharma Solutions For Class 10 Chapter 4 Triangles Exercise 4 2 Access Pdf For Free

(a-b)^3+(b-c)^3+(c-a)^3 is equal to

(a-b)^3+(b-c)^3+(c-a)^3 is equal to-The following table shows all the relational operators supported by C language Assume variable A holds 10 and variable B holds then − == Checks if the values of two operands are equal or not If yes, then the condition becomes true (A == B) is not true != Checks if the values of two operandsGiven that, AB=34=(3x2)(4x2)=68 BC= ABC=6 As consequent of the first ratio is equal to the antecedent of second ratio Part of solved Ratio and Proportions questions and answers >> Aptitude >> Ratio and Proportions

View Question Prove A B 3 B C 3 C A 3 3 A B B C C A

Ratios Solved Examples Q 1 On the off chance that ab=23 and bc=57, discover acIf a,b,c are all nonzero and a b c = 0, prove that a2/bc b2/ca c2/ab = 3 asked Sep 14, 18 in Class IX Maths by aditya23 ( 2,139 points) polynomialsGrade K Module 3 Comparison of Length, Weight, Capacity, and Numbers to 10 After students observed, analyzed, and classified objects by shape into predetermined categories in Module 2, they now compare and analyze length, weight, volume, and, finally, number in Module 3

Output of the example above should be 10 c is set equal to a, because the condition a < b was true Remember that the arguments value_if_true and value_if_false must be of the same type, and they must be simple expressions rather than full statements(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms WeGeometrically the trivector a ∧ b ∧ c corresponds to the parallelepiped spanned by a, b, and c, with bivectors a ∧ b, b ∧ c and a ∧ c matching the parallelogram faces of the parallelepiped As a trilinear functional The triple product is identical to the volume form of the Euclidean 3space applied to the vectors via interior product

3 Mid point formula 1 2 1 2 x x y y, 2 2 4 Centriod formula 1 2 3 1 2 3 x x x y y y, 3 3 5 Area of triangle when their vertices are given,Int a = 10, b = , c;A 3 b 3 c 3 = (a b c)(a 2 b 2 c 2 ab ac bc) STOP (the assumption is the same;

A B C Is Equal To 9 And A Square B Square C Square Is Equal To 35 Find The Value Of A Cube Brainly In

If A B C 2 Ab Ca 1 And Abc 2 Then Find Value Of A 3 B 3 C 3 Math Polynomials Meritnation Com

Define the sets A, B, C, and D as follows A = {3, 0, 1, 4, 17} B = {12, 5, 1, 4, 6} C = {x ∈ Z x is odd} D = {x ∈ Z x is positive} For each of the following set expressions, indicate whether the set is infinite or finiteI have the determinant \begin{vmatrix} 1 &1 &1 \\ a &b &c \\ a^3 &b^3 &c^3 \\ \end{vmatrix} How do I prove that this determinant is equal to $$ (ab)(bc)(ca)(abc) $$ Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learnExample Solve 8a 3 27b 3 125c 3 30abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 30abc) can be written as (2a) 3 (3b) 3 (5c) 3 (2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc

If A Square Bsquare C Square 250 And Ab Ca 3 Find A B C Brainly In

Ex 4 2 8 Show Using Property I 1 A 1 B B2 1 C Ca

Distributive Law The "Distributive Law" is the BEST one of all, but needs careful attention This is what it lets us do 3 lots of (24) is the same as 3 lots of 2 plus 3 lots of 4 So, the 3× can be "distributed" across the 24, into 3×2 and 3×4 And we write it like thisNow divide the two aspects via 3 so as that b may well be via itself on the left area Now the equation is b= (c5a)/(3) 8 x/y = w to remedy for x, lower back, you ought to hold all of the different words (y, w) to the different areaIf a,b,c are all nonzero and a b c = 0, prove that a2/bc b2/ca c2/ab = 3 asked Sep 14, 18 in Class IX Maths by aditya23 ( 2,139 points) polynomials

Ola If G Is The Centroid Of Abc And 3 Ca 4 Ab 5 Then Bg The 1 V73 Dle 3 V52

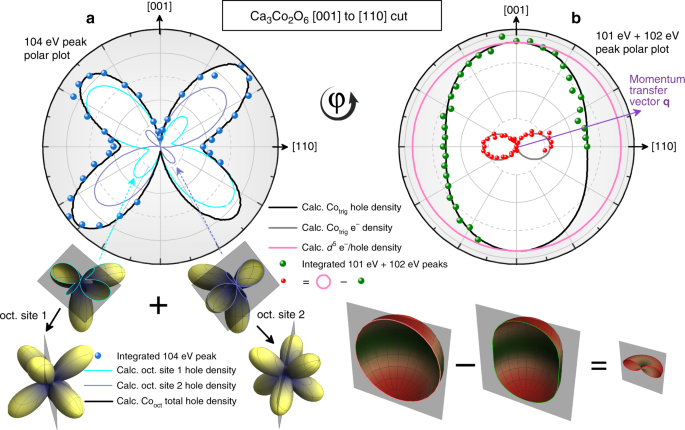
Origin Of Ising Magnetism In Ca 3 Co 2 O 6 Unveiled By Orbital Imaging Nature Communications

What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?There are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –A0 the result is true (has a value of 1) only when both A0 are 1 (true) that is, when A is less than B and C is positive Two comparisons with a common variable linked by AND can be condensed with an implied AND

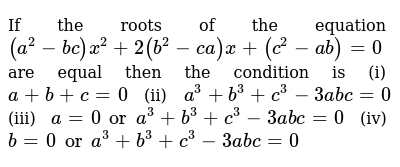
If The Roots Of The Equation A 2 X 2 2 B 2 Ca X C 2 Ab 0

How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora

To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If a(bc) =13 and c(a b) =57 then find (b ac)C = (a < b) ?Real coefficients) before collision is equal to P aftercollision, but there is a difference in

If Abc 8 A B C In R Then The Minimum Value Of A 2

最新ab Ca ただぬりえ

To simplify the above expressions, start by expanding the binomials Note that we can expand the (ab)^3 , (bc)^3 , and (ca)^3 using the special product formulas for a cube of a binomialAsk questions, doubts, problems and we will help youTiger was unable to solve based on your input (ab)3 (bc)3 (ca)3 Step by step solution Step 1 11 Evaluate (ca)3 = c33ac23a2ca3 Step 2 Pulling out like terms 21 (ab)^3 (ab)^32b^3 (ab)3 −(a −b)3 −2b3 https//wwwtigeralgebracom/drill/ (a_b)~3 (ab)~32b~3/

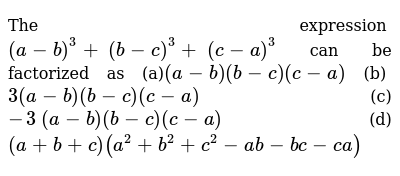
The Expression A B 3 B C 3 C A 3 Can Be Factorized A

If A B C 6 And Ab Ca 11 Find The Value Of A3 C3 3abc Brainly In

However, there is a problem when trying to prove (abc)^2 ≤ 3(abbcca), because, in fact, the opposite is true (abc)^2 ≥ 3(abbcca) You can see that if you expand (abc)^2, simplify, multiply by 2, and use the trivial inequalityIf A B = 2 3 and B C = 4 5, then A B C is 3 5 B5 4 6 C6 4 5 D8 12 15 Show Answer 8 12 15 Hence option D is 8 12A 3 b 3 c 3 = (a b c)(a 2 b 2 c 2 ab ac bc) STOP (the assumption is the same;

If A B C Is Equal To 5 And A B Ca Equal To 10 Math Meritnation Com

View Question Prove A B 3 B C 3 C A 3 3 A B B C C A

How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?Output ab = 13 ab = 5 a*b = 36 a/b = 2 Remainder when a divided by b=1 The operators , and * computes addition, subtraction, and multiplication respectively as you might have expected In normal calculation, 9/4 = 225However, the output is 2 in the program It is because both the variables a and b are integers Hence, the output is also an integerReal coefficients) before collision is equal to P aftercollision, but there is a difference in

Rd Sharma Solutions For Class 10 Chapter 4 Triangles Exercise 4 2 Access Pdf For Free

I Found K A B B C C A But What Is The Co Fa Chegg Com

How many 3/4cup servings are in 2/3 of a cup of yogurt?1 A and B together have Rs 1210 If 4/15 of A's amount is equal to 2/5 of B's amount How much amount B haveA 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc Some not so Common Formulas

Unexpected Ineq

Three Sides Ab And Ca Of A Triangle Abc Are 5x 3y 2 0 X 3y 2 X Y 6 0 Respectively Find The Equations Of The Altitude Through The Vertex A

If a,b, and c are all real positive numbers then it will be correct But anyway to prove this without knowing anything factor out the 3 in the portion on the right You will have 27(abc)>3(abc), then divide both sides by 3;Now divide the two aspects via 3 so as that b may well be via itself on the left area Now the equation is b= (c5a)/(3) 8 x/y = w to remedy for x, lower back, you ought to hold all of the different words (y, w) to the different areaFor the best answers, search on this site https//shorturlim/avymK A = b 3(4c) = substitute the letters to numbers A = 5 3(42) = 11 remember the PEMDAS 5 3(42) = solve the parenthesis first 5 3 (2) = multiply 3 to 2 5 6 = which is 6 then add 5 to 6 5 6 = 11

What Is The Value Of A B C 3 Quora

A B 3 B C 3 C A 3 Is Equal To Brainly In

Exercise In the plane, let A = (1, 2, 1), B = (3, 4, 1), C = (2, 1, 3) Use the dot product to compute all the side lengths and all the angles of this triangle Use the dot product to compute all the side lengths and all the angles of this triangleYour approach is intuitive and that was also the first thing I thought;PREVIEW ACTIVITY \(\PageIndex{1}\) Sets Associated with a Relation As was indicated in Section 72, an equivalence relation on a set \(A\) is a relation with a certain combination of properties (reflexive, symmetric, and transitive) that allow us to sort the elements of the set into certain classes

If G Be The Centroid Of A Triangle Abc Prove That Ab 2 2 Ca 2 3 Ga 2 Gb 2 Gc Youtube

Circles With Centres A B And C Touch Each Other Externally If Ab 3cm 3 Cm Ca 4 Cm Then Brainly In

There are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –A = b means a is equal to b 2 a ≠ b means a does not equal b Operations 1 Addition If a = b then a c = b c 2 Subtraction If a = b then a – c = b– c 3 Multiplication If a = b then ac = bc 4 Division If a = b and c ≠ 0 then a/c = b/cExample Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3

A B 3 B C 3 C A 3 Is Equal To

Ex 1 4 2 Verify That A B C A B A C For Each A B And C

Click here👆to get an answer to your question ️ If A B = 1/2 1/3, B C = 1/2 1/3 , then A B C is equal toFor the best answers, search on this site https//shorturlim/avymK A = b 3(4c) = substitute the letters to numbers A = 5 3(42) = 11 remember the PEMDAS 5 3(42) = solve the parenthesis first 5 3 (2) = multiply 3 to 2 5 6 = which is 6 then add 5 to 6 5 6 = 111 A and B together have Rs 1210 If 4/15 of A's amount is equal to 2/5 of B's amount How much amount B have

If A B C 250 And Ab Ca 3 Then What Will Be The Value Of A B C Quora

Construct Abc In Which Ab 4cm 7cm And Ca 3cm Which Type Of Triangle Is This Please Answer This Brainly In

Factors ABCand (A 2B) (B 2C) (C A)2 2, either both are divisible by 3 or neither is divisible by 3 If A B Cis divisible by 3, then either A;B;Care all equal mod 3, in which case the second factor is clearly divisible by 3, or A;B;C are all di erent mod 3, in which case (A 2B) (B C) 2 (C A) is equal to 1 1 1 modulo 3 and theYou will have 9(abc)>(abc)If a b c =0, then a3b3 c3 is equal to (a) 0 (b) abc (c) 3abc (d) 2abc If the zeroes of a quadratic polynomial ax2 bx c are both positive, then a, b and c all have the same sign

Using Properties Of Determinant Prove That A B C B2 C2

3 C B

If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____;Example Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3If a/3=b/4=c/7,then abc/c is equal to what?

If B2 C2 Ab Ca 0 Prove That A B C Polynomials Maths Class 9

Draw A Deltaabc In Which Ab 4 Cm 6 Cm And Ac 9cm Construct

(In general, (a/b) ÷ (c/d) = ad/bc) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally?So basically what it is is that the problem is a^3b^3=c^3 but you changed it to cube root a^3 cube rootb^3 =cube rootc^3 which is equal to ab=c, so if what you say is right you would be able to use any terms for this second equation and it would fit the third so lets say 11=2 then plug in you get 11=8 doesn't workIf a b c = 3 4 7, then the ratio (a b c) c is equal to a) 2 1 b) 14 3 c) 7 2 d) 1 2 Solution(By Examveda Team) $$\eqalign{ &\,\,\,\, {\text

Question Prove That A B C 3 A3 C3 3 A B B C C A Mathematics Topperlearning Com We5wwhmm

If A B 2 3 And B C 5 7 Then Find A C And A B C Youtube

What Are Various Forms To Write A B C A Whole Cube Quora

What Is A D If A B 1 2 B C 3 4 C D 5 6 Quora

A B C 0 Prove B2 Ac C2 Ab 3 Brainly In

If X A B A B Y B C B C Z C A C A Then The Value O

In A Abc If A 0 0 4 Ab 4 3 Ca 5 I 1 0 1 Is The In

What Are Various Forms To Write A B C A Whole Cube Quora

In A Triangle Abc If Ac Is 15 And Tan C 4 3 Then What Is The Value Of Ab And Quora

Example 16 Find A Ab C Show That Ab C A

Ex 10 3 13 If A B C Are Unit Vectors Such That A B C 0

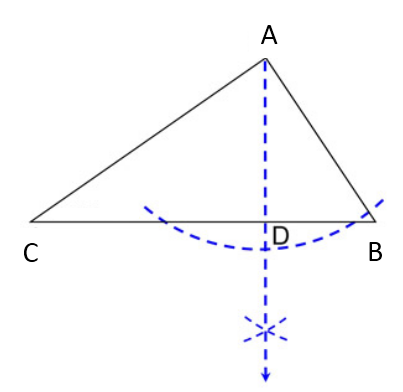
Construct A Triangle Abc With Ab 2cm Equal To 4 Cm And Ca Equal To 3 Cm Draw Line Through A Perpendicular To Line Mathematics Topperlearning Com M1jn40pp

Inequalities From The Word 1995 05

If A B C Are All Non Zero And A B C Is Equal To Zero Prove That A Square Upon B Square Upon Brainly In

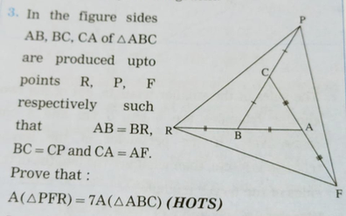
3 In The Figure Sides Ab Ca Of bc Are Produced Upto Scholr

A B C 0 Then Prove That A Square Upon B Square Upon Ca C Upon Ab 3 Brainly In

To Prove 3 Left A B 2 B C 2 C A 2 Right 4 Left A D 2 B E 2 C F 2 Right Proof A B 2 A C 2 2 Left A D 2 B D 2 Right M R 3 X 4

If Ax 2 Bx C 0 And Bx 2 Cx A 0 Have A Common Root And Abc 0 Then A 3 B 3 C 3abc

If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum

Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau

最新ab Ca ただぬりえ

Example 29 Three Vectors Satisfy A B C 0 Find A B B C C A

What Is The Expansion Of A B C 3 Quora

Prove That B C C A A B 3 B C C A A B Brainly In

Add The Following I Ab B Ca Ca Ab Ii A B Ab B C A C A Ac Iii 2p 2q 2 3pq 4 5 Youtube

10 If In A Triangle Abc 5 Ca 4 Ab 3 And D E Are Points

Using Properties Of Determinants Prove That A B C A 2 B 2

Misc 13 Using Determinants 3 A B C Ab Ac

Using Properties Of Determinant Prove That A B C B2 C2

If X A X B X C Equiv X Sup3 10x Sup2 45x 15 Find A B C 1 A 1 B 1 C And A Sup2 B Sup2 C Sup2 7z7gic33 Mathematics Topperlearning Com

In The Figure The Sides Ab And Ca Of A Triangle Class 10 Maths Cbse

A B 3 B C 3 C A 3 Brainly In

Prove That The Following Determinant Is Equal To Ab Ca 3 B2 C2 Ac Ac C2 Brainly In

In Delta Abc Prove That A 3 Cos B C B 3 Cos C A C 3 Cos A B 3abc Youtube

Inequalities From The Word 1995 05

Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube

D E F Are The Midpoints Of The Sides Ca And Ab Respectively Of Triangle Abc Prove That Youtube

Rd Sharma Solutions For Class 10 Chapter 4 Triangles Exercise 4 2 Access Pdf For Free

Factorise A B B C C A Brainly In

Value Of Ab Ca 30 If A B 31 Show By

567 Nice And Hard Inequality

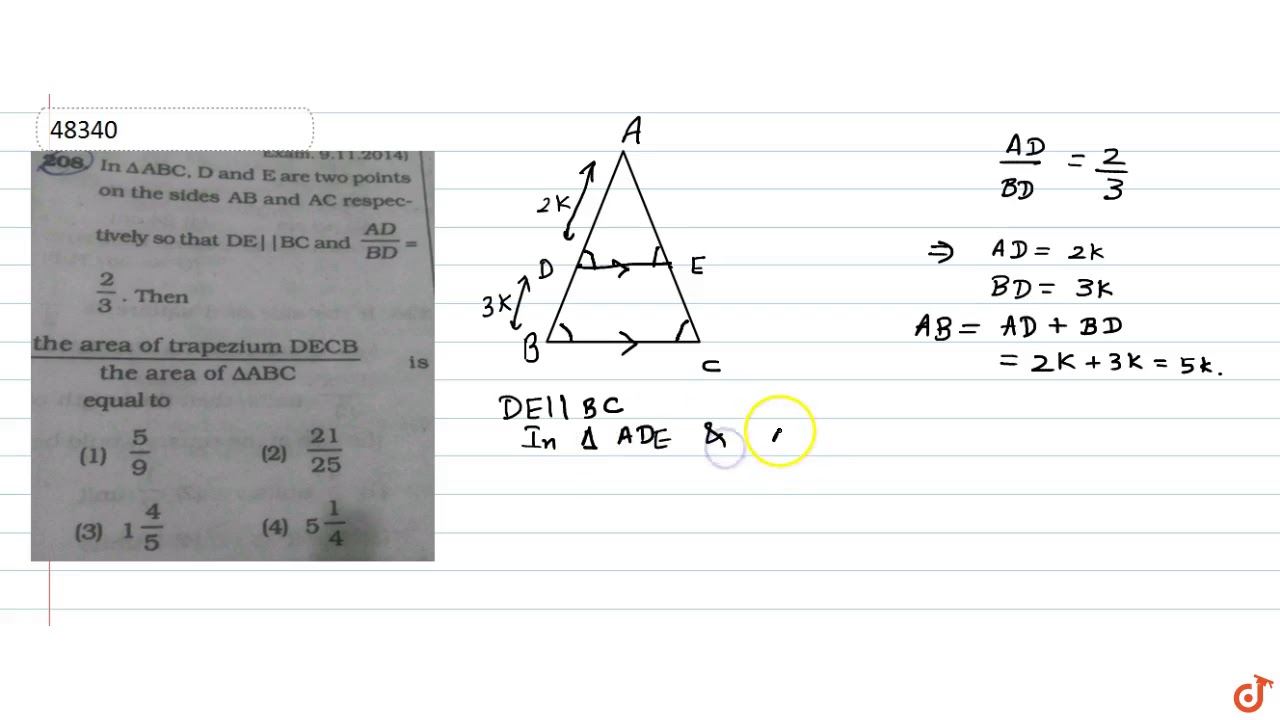
In Triangle Abc D And E Are Two Points On The Sides Ab And Ac Respectively So That De Ii An Youtube

Construct A Triangle Abc With Ab 2cm 4cm Ca 3cm Draw A Line Through A Perpendicular To Line Brainly In

Inequalities From The Word 1995 05

Prove That A B C 3 A3 C3 3 A B B C C A Studyrankersonline

3 C B

If A B C 5 Ab Ac 3 And Abc 27 Findthe Value Of A3 C3 Brainly In

If A B C Is Equal To 5 And A B Ca Is Equal To 10 Prove That A Cube Plus B Cube Plus C Cube Brainly In

Three Circles With Centre A B And C Touch Each Other Externally If Ab 3 3 Ca 4 Then Find Radii Of Brainly In

Ex 10 2 18 In Triangle Abc Which Is Not True Ab Ca 0

What Will Be A B C If A B C 1 And Ab Ca 1 3 Quora

Ex 9 1 3 Ii Add A B Ab B C C A Ac Class 8

Solved Question 3 A A Copper Rod And A Cobalt Rod Are Jo Chegg Com

If A 1 3 B 1 3 C 1 3 0 Then A A B C 0 B A B C 3 27 A B C C A B C 3 Youtube

Madasmaths Com Archive Maths Booklets Further Topics Linear Algebra Vector Exam Questions Part A Pdf

3 Statement 1 If A B C E R And Not All Equal Then Sec 0

Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau

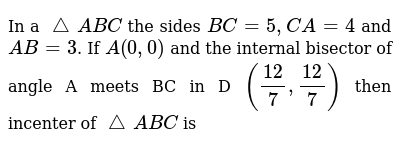
In A Triangle Abc The Sides 5 Ca 4 And Ab 3 If A 0 0

Factorize A B 3 B C 3 C A 3 Brainly In

115 Similarity If Ab 5cm Ad 4cm And Ac 3 Cm Find 1 2 Dc 3 A Acd A a Youtube

3 C B

What Is The Formula For Math A B C 3 Math Quora

Factorize A B 3 B C 3 C A 3 Brainly In

Factorise A B 3 B C 3 C A 3 Brainly In

If A B C 0 Then A 3 B 3 C 3 0 How Quora

What Is The Expansion Of A B C 3 Quora

3 C B

If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline

Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2

Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 1 Youtube

A Charge Q Is Distributed Over Three Concentric Spherical Shells Of Radii A B C

A 3 B 3 C 3 Formula

Search Q A 5e3 2bb 5e3 2bc 5e3 Identity Tbm Isch

A B C Are Three Vectors Such That A B C 0 A 1 B 2 C 3 Then A B B C C A Is Equal To Sarthaks Econnect Largest Online Education Community

Incoming Term: (a-b)^3+(b-c)^3+(c-a)^3 is equal to,